4-10. A beam is subjected to a
normally distributed load 
lb and a
normally distributed moment 
in·lb as
shown. If the maximum allowable shear stress is 
psi,
what is the minimum cross sectional area of the beam with a probability of
failure of 10-4 due to excessive shear stress? If the maximum
allowable bending stress is 
psi, then
what is the probability of failure due to excessive normal stress if you assume
the beam has a square cross section. Assume 
,
, 
,
and 
are independent.
 |
Solution:
Sum the forces: Find the maximum shear stress that is developed by summing the forces in the
direction and take the
moment about 
.
 |
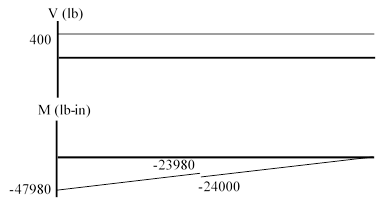
The maximum shear is 
and
the maximum moment is at point with magnitude
.
Shear Stress: Calculate the maximum shear stress in
the beam due to.
psi (1)
psi (2)
psi
Probability of failure:
(3)
Since lb and 
psi are independent, Y also follows a normal
distribution. 
.
psi (4)
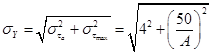psi (5)
Equation (3) can be written as
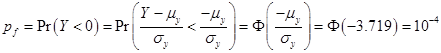
From (3), (4), (5), and some algebra we obtain
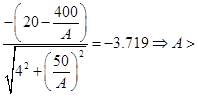32.9973 in2
~ 
in2 Ans.
Assume
square cross sectional area: 
and 
.
Moment of inertia: Calculate the moment of inertia about the x axis.
in4
Bending stress: Calculate the distribution of stress that is developed in the beam.
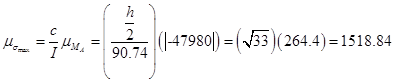psi
(6)
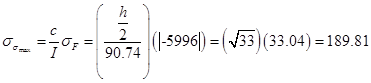psi
(7)
psi
Probability of failure:
(8)
Since psi and psi are independent, Y also follows a normal
distribution. .
psi
(9)
psi (10)
Equation (8) can be written as
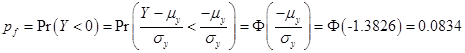Ans.