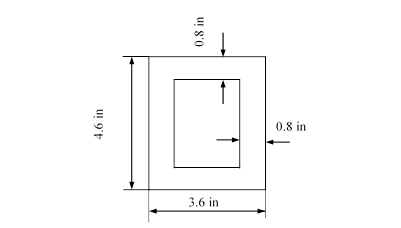
8-15. A 14-ft long tube is fixed at both ends. The cross-sectional area of this tube is shown in the figure. If the modulus of elasticity follows . Determine the distribution of the critical axial buckling load. If the axial load acting on the column folllows , determine the probability of failure. Assume that E and P are independent and Euler’s formula is available.

Solution:

The section property is

Then, the critical axial buckling load is

;       .

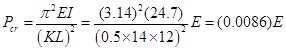Since , we have

Thus, the critical axial buckling load follows .                                      Ans.

Set , then , where

Thus, the probability of failure is

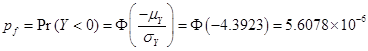                     Ans.