8-2.  A rod is subject to two forces as shown. The rod is 16 in. long and its diameter is . The yield strength of the rod is . The modulus of elasticity follows a normal distribution . The forces also follow a normal distribution . Find the probability of failure of the rod caused by buckling. Assume that  and are  are independent.

Solution:

The moment of inertia of the rod is , and the effective length factor . Thus, the critical buckling load of the bar can be calculated by

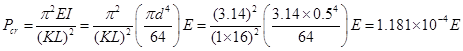
Set , then , where

Thus, the probability of failure of the rod caused by buckling could be obtained by

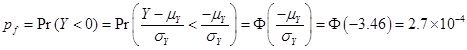Ans.