8-3. The steel bar AB with a rectangular cross section is pin connected at its ends. The distributed load q acting on BC follows a normal distribution , and the modulus of elasticity follows . The yield strength of the bar follows . Determine the probability of falure of the bar caused by buckling. Assume that E and q are independent, and Euler’s formula is valid only if the probability of failure caused by yield failure is less than 10^-6.

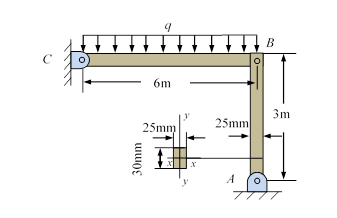
Solution:

From the free body diagram of the bar BC

,  

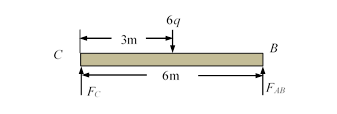
Then, we can obtain .

The effective length factor . The moment of inertia of the rod is

Thus, the critical buckling load of the bar can be calculated by

Set , then , where

Thus, the probability of failure of the rod caused by buckling could be obtained by

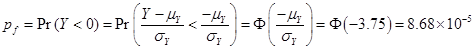Ans.

Check:

Thus,                                  

Set , then , where

,  

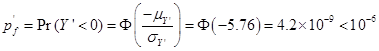OK.