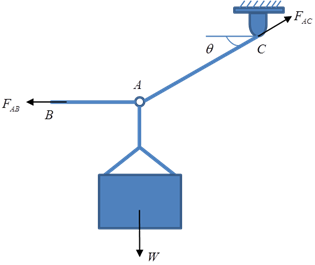
10. The weight of the crate follows a normal distribution and the crate is hoisted using ropes AB and AC. Each rope can withstand a maximum tension before it breaks. If AC always remains horizontal and is , determine the probability that rope AB and AC will break. Note all the forces , , , and are independently distributed.

Solution

For and

So the distributions of F_AC and F_AB are and , respectively.

We know the maximum tension of each rope is before it breaks, suppose

Thus

So the distributions of Y and Z are and , respectively.

The probability of the break of rope AC is and the probability of the break of rope AB is,

Ans.

Ans.

Thus, we conclude that the probability of the break of rope AC is 0.129 and the probability of the break of rope AB is 0.015.