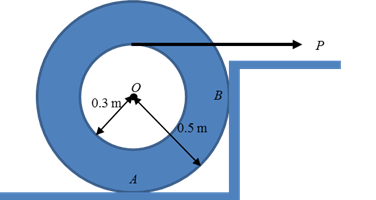
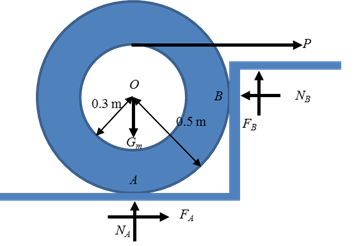
4. The spool rests on the ground at A and against the wall at B. The weight of the spool follows a distribution m ~ N(130,4.5²) kg due to the manufacturing uncertainty. (1) Determine the maximum force P so that the probability of no motion is less than 0.01%. (2) If the strength of wire, which is independent of m, exerted on the spool follows another normal distribution T ~ N(700, 6²) N, determine the probability that the wire may break when force P begins pulling the wire horizontally off the spool. The coefficient of static friction between the spool and its position of contact is µ_s=0.2.

Solution

Where and .

Solving the above equations, with m ~ N(130,4.5²) kg, we can obtain

Thus, we have the distribution: P~ N(659.64, 22.83²) N.

Therefore, the maximum magnitude P so that the probability of no motion is less than 0.01% can be computed by the underneath equation inversely

Finally, we have P_max=744 N. Ans.

(2) The distribution of the wire strength is T ~ N(700, 6²) N. Therefore, we could have

The probability that the wire may break is

Ans.