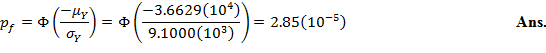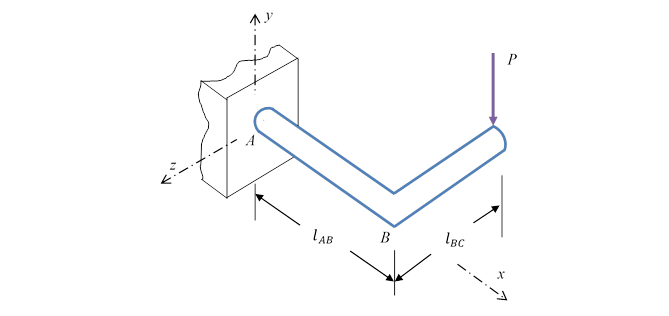
22. A crank shown in the figure is subjected to a force . The shaft  is fixed at  and has a diameter of . The length of the shaft  is , and the length of the arm  is . The yield strenght of the shaft  is . If  and  are independent, estimate the probability of failure using the First Order Second Moment Method. Use the distortion-energy theroy.

Solution

Draw a free-body diagram of the shaft  and the critical stress element appearing on the top surface at point A.

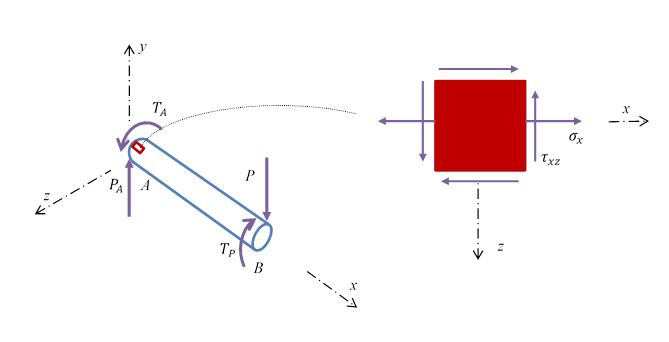
For the critical stress element, the normal stress resulted from the bending moment is found to be

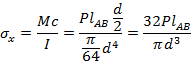
And the shear stress resulted from torsion is given by

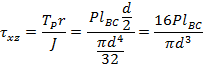
where  is the torsion resulted from the force ,  is the radius of the circular cross-section, and  is the polar second moment of inertial.

Based on the distortion-energy theory, the von Mises stress is

So the limit-state function is the von Mises stress subtracted from the yield strength. Failure occurs when.

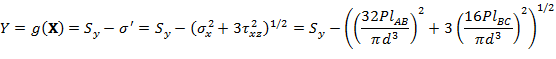
where .

Using FOSM, we have

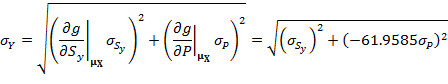
The probability of failure is then given by