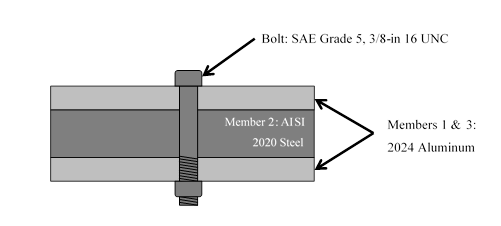
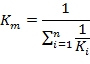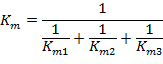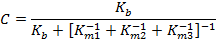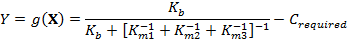4. A joint is required to have a stiffness coefficient C less than 0.30 or a failure will occur. The joint consists of a 1-in thick steel plate between two identical 1/2-in thick aluminum plates held together by a 3/8-in 16 UNC bolt and a nut. All the stiffness constants are random vraribales as shown in the table. Find the probablity of failure for the joint using Monte Carlo Simulation. Assume that all stiffness constants are independent.

Random Variable	Type	Mean (µ)	Std. Dev. (σ)	Units
K_b (bolt stiffness)	Normal	1.75	0.075	Mlb/in
K_m1 (member 1 stiffness)	Normal	7.5	0.1	Mlb/in
K_m2 (member 2 stiffness)	Normal	43	1	Mlb/in
K_m3 (member 3 stiffness)	Normal	7.5	0.1	Mlb/in

Solution

The stiffness constant for the members in series is the inverse of the sum of their inverses.

(1)

Plugging in the given known random variables, Equation (1) yields Equation (2)

(2)

The stiffness coefficient of the joint is simply the ratio of stiffness of the bolt to the sum of the bolt and member stiffness.

		(3)
		(4)

The limit-state function is simply the required stiffness constant subtracted from the actual stiffness constant value. Failure occurs when Y < 0 (when the actual stiffness is less than the required stiffness).

(5)

X denotes the vector of values of , , , and .

Using Monte Carlo Simulation and 1e7 samples, the probability of failure is found to be 1.7930e-04. Ans.