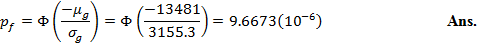2. A solid circular rod is subjected to an axial force of . The yield stress of the rod is . The factor of safety is . a) What is the minimum diameter of the rod? Then select a preferred fractional diameter. b) If , , and P and S are independent, determine the probability of failure using the First Order Moment Method.

Solution

a)  The cross-sectional area of the rod is

     The tensile stress of the rod is

     The tensile stress should be less than the allowable stress

     Solving for  yields

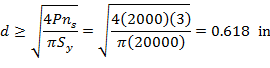
     Thus the minimum diameter of the rod is 0.618 in.                                                                                                       Ans.

And the preferred fractional diameter could be chosen as  in = 0.625 in.                                                          Ans.

b)  The limit-state function is the actual stress of the rod subtracted from the allowable maximum stress.   

      Failure occurs when

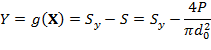
     where , and = 0.625 in is the preferred diameter.

     Using FOSM, we have

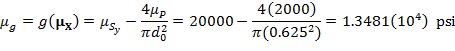
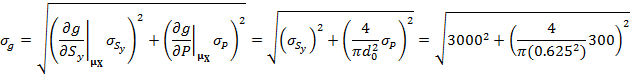
      Evaluate the probability of failure