3. The allowable shear stress of a shaft is , and the shaft speed is  rev/min. a) What is the minimum diameter of the shaft to transmit 50 KW? Then select a preferred diameter. b) If  and  rev/min and  and  are independent, determine the probability of failure using Monte Carlo Simulation.

Solution

a)

The torque can be obtained from the given power and speed.

where  is the power, and  is the shaft speed.

The maximum shear stress developing throughout the cross section is

where  is the radius of the shaft,  is the diameter, and  is the polar second moment of area.

The maximum shear stress should be less than the allowable shear stress.

Solving for  yields

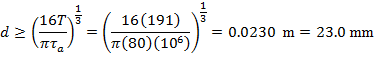
Thus the minimum diameter of the shaft is 23.0 mm.                                                                                                       Ans.

The preferred diameter could be chosen as                       Ans.

b)

The limit-state function is the actual maximum shear stress of the shaft subtracted from the allowable maximum shear stress. Failure occurs when .

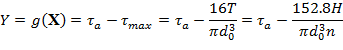
where , and = 25 mm is the preferred diameter.

Using Monte Carlo Simulation and 1e7 samples, the probability of failure is found to be 9.50(10^-6).                            Ans.