5. A shaft is fixed at point A and C. It is subjected to two toques acting at point B. The diamater of the shaft is . If , , and  and are independent, determine the distribution of the angel of twist at B.

Solution

Since the angle of twist ,

where  and are the torque reactions at A and C, respectively,  is the torsional constant,  and  is the shear modulus of steel.

Then

According to the moment equilibrium of shaft AC

Then

Thus, the angle of twist at B is

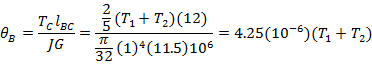
Since  and  are independently and normally distributed, their linear combination,  , is also normally distributed. The mean and standard deviation of   are given by

So the distribution of the angel of twist at B is                            Ans.

4.5