Example 7

The surface of a cam is expressed by a logarithmic spiral formula , where  is in radians. Due to the uncertainty in the manufacturing process of the cam, the coefficient  follows a normal distribution of . The cam rotates at an constant angular velocity of . Determine the distribution of the velocity and the acceleration of the point on the cam that contacts the follower rod AB at the instant . If the allowable acceleration of AB is , find the probability of failure of the system.

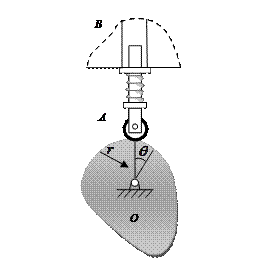
Solution:

The velocity of the contact point on the cam is calculated by

in which 

Thus,  could be rewritten as

Since ,  follows a normal distribution with

Ans.

The acceleration of the contact point on the cam is calculated by

in which 

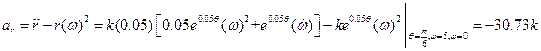
Thus,  could be represented by

which also follows a normal distribution with

Ans.

Let , the mean and standard deviation of  are then given by

Thus, the probability of failure of the cam system is given by

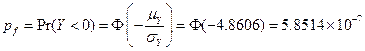Ans.