Reliability-Based Design (RBD)

A cantilever beam is subjected to two random forces  lb and  N at the tip as shown. The yield stress is  psi, the Young’s Modulus is  psi, and the allowable deflection is  in. The length of the beam is a random variable with  in. Given the minimum probabilities of  for failure modes of excessive normal stress and excessive deflection, find the optimal solution so that the volume of the beam is minimized. The ranges of the beam size are given by   and .

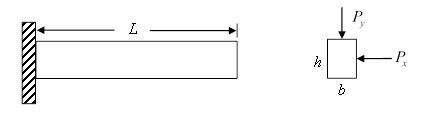
Solution

The design variable are  and ; the objective function is . The random parameters are . There are two failure modes. For the failure mode of excessive stress, the limit-state function is given by

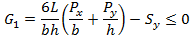
For the failure mode of excessive deflection, the limit-state function is given by

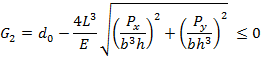
All the information we know are listed below.

 lb

 lb

psi

 in

 in

,,

 = 0.999, or

In order to find the optimal solution, we minimize  with two reliability constraints. The optimization model is given by

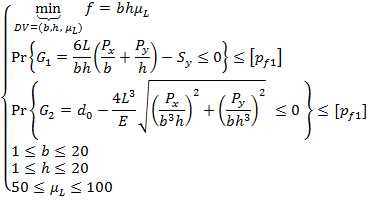
The First Order Second Moment method (FOSM) is used for reliability analysis, and Matlab is used to solve the optimization model. The optimal solution is as follows:

Design variables:

Objective function:

Probability of failure for failure mode 1:

Probability of failure for failure mode 2:

The compare RBD with deterministic optimization (only mean values are used), we give the results from both methods in the following table.

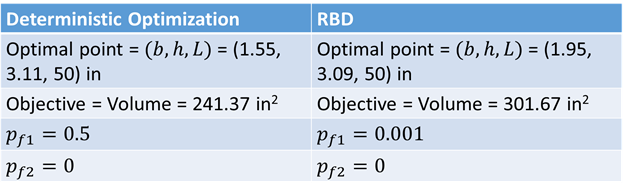
The Matlab codes are given below.

1) Main function

% Main program of RDB for a cantilever beam

% Xiaoping Du, Missouri S&T, 04/10/2017

clear all; warning off;

%----------------------- Reliability-Based Design---------------

dv0 = [2.0,3.0,40.0];                % dvs=[b,h,uL]

dvl = [1.0,1.0,50.0];                % lower bounds of dvs

dvu = [20.0,20.0,100.0];             % upper bounds of dvs

required_pf(1:2) = 0.001;    % Required probabilities of failure

options = optimset('Display','iter','MaxFunEvals',1000); % Display convergence history

dv = fmincon('rbd_obj_fun',dv0,[],[],[],[],dvl,dvu,'rbd_con_fun',options,required_pf);    

%obj_fun: function for objective

%con_fun: function for constraints

%Posterior analysis

obj = rbd_obj_fun(dv);

[g,ceq] = rbd_con_fun(dv,required_pf); %g=pf-required_pf

pf = g+required_pf;

%Display the results

disp('------------------RBD Results-------------------');

disp(['The optimal point = ',num2str(dv)]);

disp (['The objective function = ',num2str(obj)]);

for i = 1:2

    disp(['Probability of failure mode ',num2str(i),' = ',...

            num2str(pf(i))]);

end

2) Objective function

%Objective function

function f = rbd_obj_fun(dv,required_pf)

%dvs=[b,h,uL]

f = dv(1)*dv(2)*dv(3); %Volume

3) Constraint function

% Constraint functions

% FOSM is used to calculate the probability of failure

function [g,ceq] = rbd_con_fun(dv,required_pf)

ceq = [];             %No equality constraints

%d=(b,h), X=(L), P=(Px,Py,S,E)

%dv=[b,h,uL];

b = dv(1); h = dv(2); L = dv(3);

Px = 500; Py = 1000; S = 4.0e4; E = 29.0e6; %Mean

sL = 0.1; sPx = 100; sPy = 100; sS = 2.0e3; sE = 3.0e6; %Std

%Calculate mean of g

ug1 = S-6*L/b/h*(Px/b+Py/h);

ug2 = 2.5-4*L^3/E*((Px/b^3/h)^2+(Py/b/h^3)^2)^0.5;

%Calculate std of g

dg1dL = 6/b/h*(Px/b+Py/h);

dg1dPx = 6*L/b/h/b;

dg1dPy = 6*L/b/h/h;

dg1dE = 0;

dg1dS = 1;

dg2dL = -12*L^2/E*(Px^2/b^6/h^2+Py^2/b^2/h^6)^(1/2);

dg2dPx = -4*L^3/E/(Px^2/b^6/h^2+Py^2/b^2/h^6)^(1/2)*Px/b^6/h^2;

dg2dPy = -4*L^3/E/(Px^2/b^6/h^2+Py^2/b^2/h^6)^(1/2)*Py/b^2/h^6;

dg2dE = 4*L^3/E^2*(Px^2/b^6/h^2+Py^2/b^2/h^6)^(1/2);

dg2dS = 0;

stdg1 = ((dg1dL*sL)^2+(dg1dPx*sPx)^2+(dg1dPy*sPy)^2+(dg1dE*sE)^2+(dg1dS*sS)^2)^0.5;

stdg2 = ((dg2dL*sL)^2+(dg2dPx*sPx)^2+(dg2dPy*sPy)^2+(dg2dE*sE)^2+(dg2dS*sS)^2)^0.5;

%Calculate reliability

pf(1) = normcdf(-ug1/stdg1);

pf(2) = normcdf(-ug2/stdg2);

%Constraints

g(1) = pf(1)-required_pf(1); %Matlab uses g<=0

g(2) = pf(2)-required_pf(2);