Homework 1

Uncertainty Modeling: Probability

1. With statistical data on 1000 machines operated in factory A, the reliability of the machine is estimated to be 0.99. Statistics from factory B shows that 5 machines failed out of 600 machines operated in factory B. Based on the statistics from both factories, what is the reliability of the machine.

2. 70% failures of the blades of a wind turbine are due to fatigue, and 20% due to excessive bending. If the probability of failure due to both failure modes is 10%, what is the probability of failure of the blades?

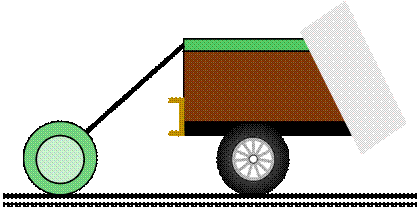
3. The strength of the cables made a company is tested in repeated experiments where a pipe is towed behind a truck through the cable. The experiments result in the following probabilities. The probability that the cable breaks before it starts to move is 0.6, and the probability that the cable breaks after it has started to move is 0.7. What is the probability that the cable will break? Resolve the problem if the two probabilities are 0.01 and 0.02.

4. In the process of manufacturing a mechanical component made of a composite material, voids defect and bonding defect occur with probabilities 0.01 and 0.02, respectively. If these two defects occur independently, determine

(a) the probability that the component is free of both types of defects, and

(b) the probability that the component has at least one defect of either type.

5. The failure of a component cannot be observed directly, and a sensor is designed to detect the failure. Statistical data indicate that the probability of failure of the component is 0.1%. When the component fails, an alarm, which indicates a failure, is activated by the sensor 99% of the time. When the component does not fail, the sensor activates an alarm 2% of the time.

(a) What is the probability that the alarm is activated?

(b) If the alarm is activated, determine the probability that the component actually failed.

6. The probabilities that the external force Q acts in locations M and N are 0.6 and 0.4, respectively. If Q acts at M, the probabilities of failure due to bending and shear are 0.001 and 0.0001, respectively. If Q acts at N, the probabilities of failure due to bending and shear are 0.002 and 0.0001, respectively. The probability of both bending and shear failures is 0.00008. Determine (1) the probability of bending failure, (2) the probability of shear failure, (3) given that bending failure occurred, the probabilities that the force Q acts at M and N, respectively, and (4) the reliability of the beam.

7. A pumping system on an oil field consists of three pumps as shown below. The reliabilities of the individual pumps are . The states of the pumps are independent.

(1) Please calculate the reliability and the probability of failure of the system.

(2) Assume that the cost of improving reliability of each pump is the same. If a higher system reliability is desired and the reliability of only one pump can be improved due to the cost concern, which pump should be improved in terms of reliability?

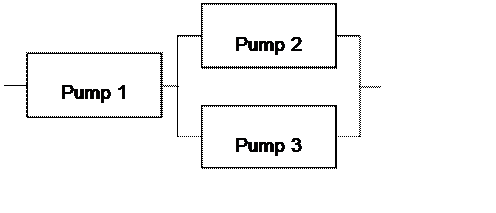
8. A system consists of four identical components with the same component reliability. The system must work even one component fails, and the system reliability should be 0.99999. Assume that the cost of each component is directly proportional to the component reliability. (1) What are the possible system configurations you may use? Only consider series, parallel, or mix systems. (2) Calculate the component reliability for all the possible systems. (3) What system minimizes the cost of purchasing the components?