Homework 2
1. During an experiment in class, a number of paper clips were bent until each failed. The numbers of cycles to failure were recoded as shown below.
19.5 18 12 13 11 40 17 18 12 14 18.5 17.5
20 15 16 18.5 29 21 23 21 19 24 18 33
28 29 58 37
(1) Calculate the average of the cycles to failure.
(2) Calculate the standard deviation of the cycles to failure.
(3) Calculate the median of the cycles to failure.
2. The angular velocity X of a shaft varies randomly with the following probability density
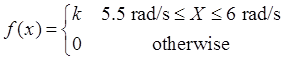
(1) What
is 
?
(2) What the mean value of the angular velocity?
(3) What is the standard deviation of the angular velocity?
(4) What the median of the angular velocity?
(5) What
is the probability 
?
(6) What is the 95% percentile value of the angular velocity?
3. A system consists of two electronic components as shown in Fig. 1.
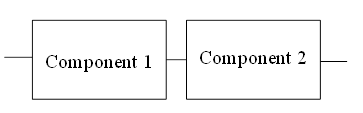
Fig 1. A system with two components
The
lives of the two components 
and 
follow the following
distributions:
where
and 
. and are independent.
(1) Determine
the joint PDF of and .
(2) Determine the reliability of the system after the system is in operation for 1000 hr.
4.
A joint of a mechanism can be considered as a journal
bearing. As shown in Fig. 2, the radius of the bearing 
is
greater than that of the journal 
. Their difference
is called a clearance, and 
. As indicated in
Fig. 3, the position 
of the center of the
journal relative to the center of the bearing is within a circle of radius 
. This circle is called a
clearance circle.
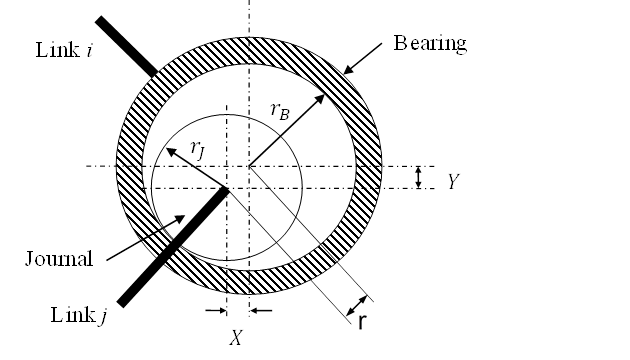
Fig. 2 Joint clearance
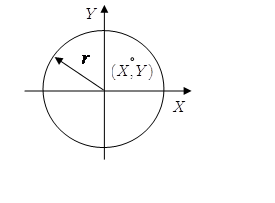
Fig. 3 Clearance circle
Assume that the clearance is known and that the position is uniformly distributed within the
clearance circle 
. (The PDF is constant
within the clearance circle .) Determine
(1)
The joint probability density function (PDF) of 
and 
(2)
The PDFs of and
(3)
The means of and
(4)
The variances of and
(5)
The coefficient of correlation between of and