Homework 3
1.
The yield strength, ![]() ,
of the material used for a mechanical component, is normally distributed with
,
of the material used for a mechanical component, is normally distributed with ![]() MPa. The stress of the component is also
normally distributed. The field statistical data of the stress
MPa. The stress of the component is also
normally distributed. The field statistical data of the stress ![]() are collected and are shown in the
following table.
are collected and are shown in the
following table.
(1) What is the deterministic factor of safety?
(2) What is the probability of failure?
(3) Among 10000 components, how many components are expected to fail?
Table
1 Observations of Stress ![]() (MPa)
(MPa)
|
77.19 |
19.94 |
|
59.11 |
99.65 |
|
61.01 |
62.03 |
|
86.09 |
83.18 |
|
51.25 |
80.85 |
|
94.52 |
75.53 |
|
89.22 |
49.90 |
|
54.45 |
51.32 |
|
68.35 |
65.63 |
|
45.30 |
45.35 |
2. The strength of a mechanical component follows a lognormal distribution with a mean of 200 MPa and standard deviation of 25 MPa.
1) What is the probability that the component will have strength less than 180 MPa?
2) What is the 95% percentile strength?
3.
A number of CAE simulations are performed for the engine slap
noise for a vehicle engine design. Through the Design of Experiments (DOE) and simulations,
the model of the noise ![]() (dB) is created with
respect to design variables
(dB) is created with
respect to design variables ![]() ,
, ![]() , and
, and ![]() as
as
![]()
in which ![]() ,
,
![]() ,
, ![]() ,
and
,
and ![]() ;
; ![]()
![]() are random variables, which are
given in the following table.
are random variables, which are
given in the following table.
Table 2 Random Variables
|
Random Variables |
Mean |
Standard Deviation |
Distribution |
|
|
65 |
5 |
Normal |
|
|
22.5 |
3 |
Normal |
|
|
0.9 |
0.1 |
Normal |
(1)
If the design requirement for the noise is ![]() dB. What is the probability that the
design satisfies the requirement?
dB. What is the probability that the
design satisfies the requirement?
(2) If the reliability (the probability of requirement satisfaction) is not satisfactory, how do you suggest improving the design?
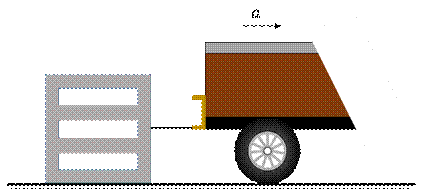
4.
A concrete block of 10,000 kg is towed by a vehicle through a
cable. The vehicle starts from rest with an acceleration of ![]() m/s2, and the
static and kinetic coefficients of friction between the block and ground are
m/s2, and the
static and kinetic coefficients of friction between the block and ground are ![]() and
and
![]() , respectively. The strength
of the cable is
, respectively. The strength
of the cable is ![]() kN. Assume all the
random variables are independent. Determine the probability that the cable
would break.
kN. Assume all the
random variables are independent. Determine the probability that the cable
would break.
5.
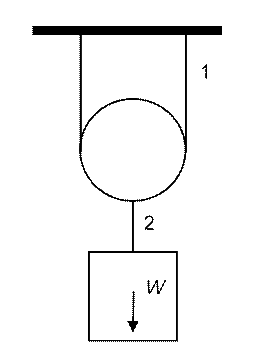 The
weight of the crate follows a normal distribution
The
weight of the crate follows a normal distribution ![]() . The allowable tensions of the two cables
are also normally distributed with
. The allowable tensions of the two cables
are also normally distributed with ![]() and
and ![]() , respectively. The three random variables
are independent. Determine the reliability of the system. (Consider only the
two cables. Neglect the weight of the pulley.)
, respectively. The three random variables
are independent. Determine the reliability of the system. (Consider only the
two cables. Neglect the weight of the pulley.)