Monte Carlo Simulation

Please attach your source code.

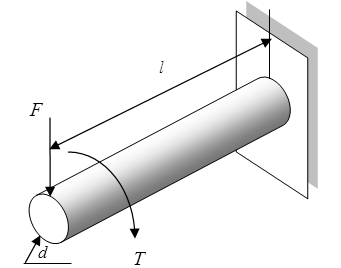
1. The limit-state function of a shaft in a speed reducer is defined by the difference between the strength and the maximum equivalent stress. It is given by

where

mm, the diameter of the shaft

 mm, the length of the shaft

 the external force

 the external torque

the yield strength

The distributions of the independent random variables are given below.

Table 1 Distributions

Variables	Mean	Std	Distribution
External force	2000 N	220 N	Normal
Torque	450 N·m	50 N·m	Normal
Strength	250 MPa	30 MPa	Normal

Use Monte Carlo simulation to calculate the probability of failure. Please give the 95% confidence interval for the MCS solution.

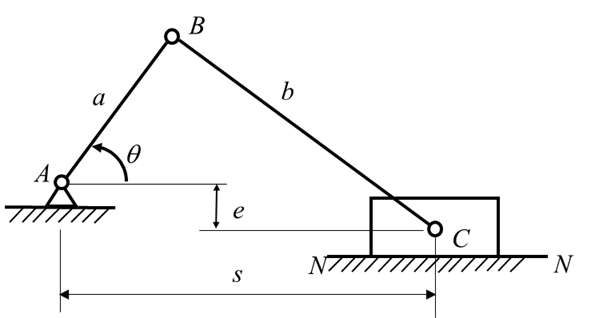
2. The position of a slider-crank mechanism  is required to be 350 mm when  . A failure occurs if the actual position  is outside the range    mm. The tolerance of the three independent dimension variables  ,  , and  is  mm. Their distributions are given in Table 2. Use Monte Carlo simulation (MCS) to calculate the probability of failure. Please give the 95% confidence interval for the MCS solution.

The distributions of the independent random variables are given below.

Table 2 Distributions

Variables	Mean	Std	Distribution
	136.6 mm		Normal
	216.8 mm		Normal
	0 mm		Normal

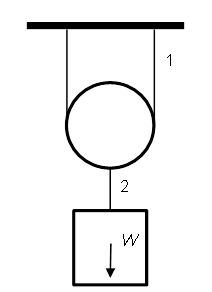
3. (This is Question 5 in Homework 3.) The weight of the crate follows a normal distribution . The allowable tensions of the cables 1 and 2 are also normally distributed with  and , respectively. The three random variables are independent. Determine the reliability of the system. (Consider only the two cables. Neglect the weight of the pulley.) Compare the simulation solution with the solution you have obtained before.